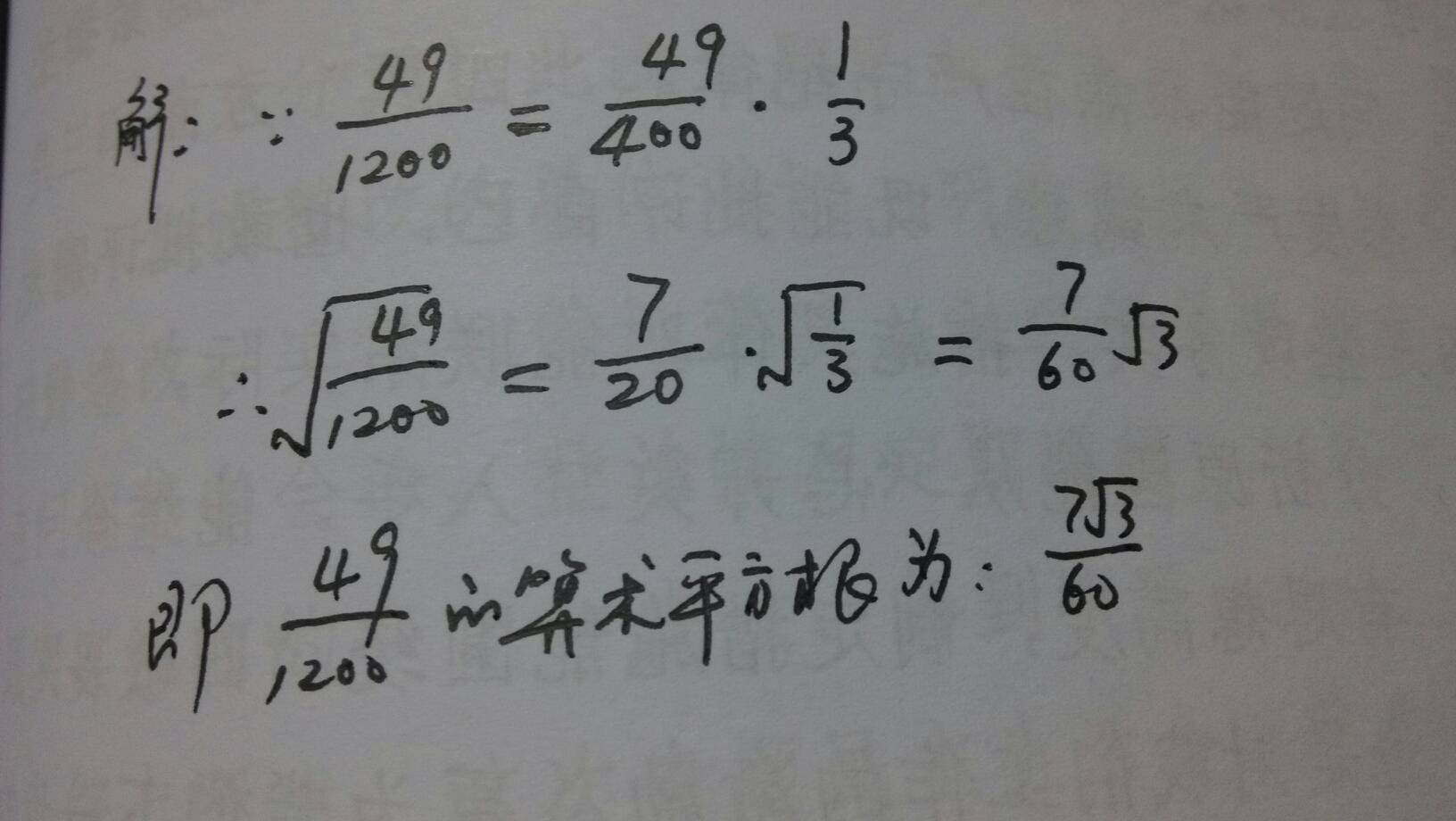二次根式的定义与性质
定义
如果一个数的平方等于a,那么这个数叫做a的平方根 a可以是具体的数,也可以是含有字母的代数式。
a可以是具体的数,也可以是含有字母的代数式。
即:若x2则 叫做a的平方根,记作x= ±√a。其中a叫被开方数。其中正的平方根被称为算术平方根。 扩展资料
性质
1. 任何一个正数的平方根有两个,它们互为相反数。如正数a的算术平方根是√a ,则a的另一个平方根为﹣ √a;最简形式中被开方数不能有分母存在。
2. 零的平方根是零,即 √0=0;
3. 负数的平方根也有两个,它们是共轭的。如负数a的平方根是±√ai 。
4. 有理化根式:如果两个含有根式的`代数式的积不再含有根式,那么这两个代数式互为有理化根式,也称互为有理化因式。
5. 当a≥0时, (√a)2=√a2,其中a取值范围是整个复平面。
6.(√a)2=a,任何一个数都可以写成一个数的平方的形式;利用此性质可以进行因式分解。
7.注意:(√a)2=丨a丨,然后根据绝对值的运算去除绝对值符号。
8.具有双重非负性,即不仅a≥0而且≥0。
零有算术平方根吗?
概念:
1.算术平方根:如果一个正数X的平方等于a,那么这个正数X就叫做a的算术平方根。
2.对零的算术平方根和平方根的特殊规定:零的算术平方根是零,零的平方根也是零。
北师大版规定0的算术平方根是0可现在的华东师大版没规定
……这不是那个版教材规定的,是国际数学协会规定的……
国际通用……
二次根式的计算结果有几个?与算术平方根有什么区别?
正数有2个平方根,它们互为相反数。
0的平方根是0.
负数没有平方根。
如果一个正数X的平方等于A,那么这个正数X叫做A的算术平方根。
0的算术平方根是0.
0有算术平方根吗?
概念:1.算术平方根:如果一个正数X的平方等于a,那么这个正数X就叫做a的算术平方根。2.对零的算术平方根和平方根的特殊规定:零的算术平方根是零,零的平方根也是零。北师大版规定0的算术平方根是0可现在的华东师大版没规定
……这不是那个版教材规定的,是国际数学协会规定的……
国际通用……
零有算术平方根吗
对零的算术平方根和平方根有一个特殊规定,就是零的算术平方根和平方根都是零。算术平方根是指如果一个正数a的平方等于X,那么这个正数a就叫做X的算术平方根。算术平方根和平方根存在的前提条件都是“只有非负数才有算术平方根和平方根”。存在包容关系:平方根包含了算术平方根,因为一个正数的算术平方根只是其两个平方根中的一个。
根号零等于多少?
√0=0。
负数没有算术平方根,实数a的算术平方根记作√a,其中a≥0,定义有√a≥0,特别规定:0的算术平方根是0。
根号的计算公式
(1)(ⁿ√a)ⁿ=a,成立条件:a≥0,n≥2且n∈N。
(2)ⁿ√aⁿ=|a|,成立条件:a≥0,n≥2且n∈N。
(3)ⁿ√a×ⁿ√b=ⁿ√ab,成立条件:a≥0,b>0,n≥2且n∈N。
(4)ⁿ√a÷ⁿ√b=ⁿ√a/b,成立条件:a≥0,b>0,n≥2且n∈N。
根式加减法法则:
二次根式加减法法则先把各个二次根式化简成最简二次根式,再把同类二次根式分别合并。
同类根式是做加减法时允许合并的诸根式,当几个根式化成最简根式后,如果它们的根指数和被开方数分别都相同,那么这些根式称为同类根式。