一、1加到1000等于多少?
1加到1000的等差数列的和=(1+1000)+(2+999)+(3+998)+(4+997)+.(5+996)+.....+(496+505)+(497+504)+(498+503)+(499+502)+(500+501)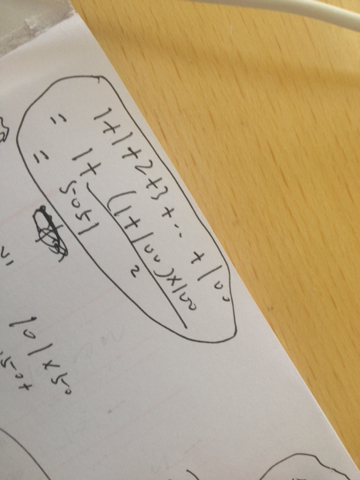 ,
,
从算式中不难看出,其中每组小括号内的和均为1001,计500组,总和是1001*500=500500.
概括起来,等差数列的求和规则是首项加末项乘以二分之一项数,一般表达式是:
Sn=a+b)*n/2,其中Sn-数列和,a,和b依次为数列的首项与末项的值,n为项数。,,
二、1加到100等于多少.,,那1加1000呢
根据计算法则,1加到1000等于首项1加上末项1000,再乘以项数1000,再除以2就是答案500500了...
三、从1一直加到100等于多少
你可以用高斯的方法呀,高斯的方法:比如1+到200,1+200=2+199=3+198…=201*100=20100 那1加到100就等于5050了
四、一加到一千等于多少?
500500。
计算公式为:(1+1000)*1000/2=500500,望采纳。
数学公式是人们在研究自然界物与物之间时发现的一些联系,并通过一定的方式表达出来的一种表达方法。是表征自然界不同事物之数量之间的或等或不等的联系,它确切的反映了事物内部和外部的关系,是我们从一种事物到达另一种事物的依据,使我们更好的理解事物的本质和内涵。
错误公式特征:
1,自称是科学的,但含糊不清,缺乏具体的度量衡。
2,无法使用操作定义(例如,外人也可以检验的通用变量、属于、或对象)。
3,无法满足简约原则,即当众多变量出现时,无法从最简约的方式求得答案。
4,使用暧昧语言的语言,大量使用技术术语来使得文章看起来像是科学的。
5,缺乏边界条件:严谨的科学理论在限定范围上定义清晰,明确指出预测现象在何时何地适用,何时何地不适用。
五、从1一直加到1000等于多少??
(1+1000)*1000/2=500500
等差数列之和=(首项+末项)×项数÷2
另外:
项数=(末项-首项)÷公差+1
末项=首项+(项数-1)×公差
公差=相邻两数之差