关于r是p的必要不充分条件
如果r是p的必要不充分条件,那么p推得出r,r推不出p,所以p属于r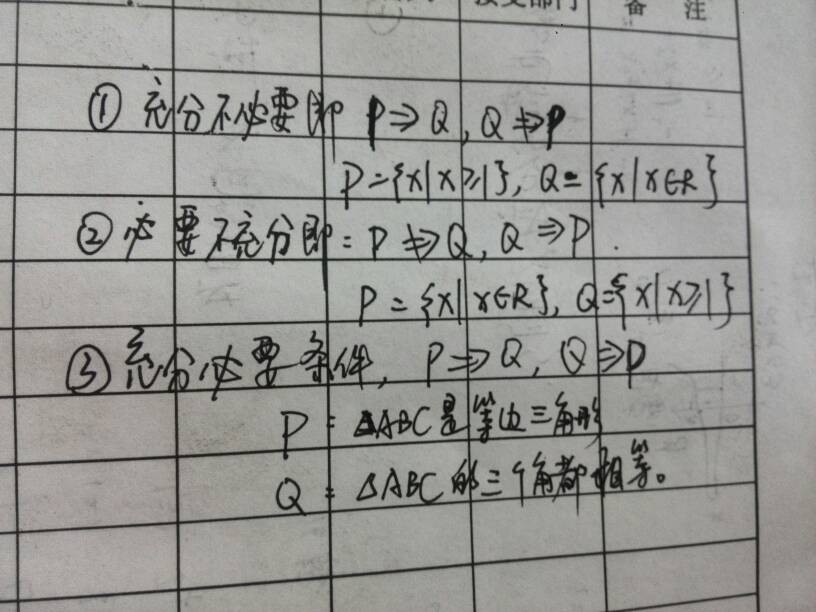
这里p是结论,r是条件,把二者关系弄清楚就很简单了。
充分条件和必要条件,还有充分不必要,必要不充分都是啥意思啊,能用通俗的一点的语言表达吗?
所谓“充分条件”,就是指条件能充分的证明结论的成立。
所以就是条件成立,必然能得到结论成立的关系。
例如“张三是小学生”这个条件能充分的证明“张三是学生”这个结论
所以“张三是小学生”就是“张三是学生”的充分条件。
“张三小学生”成立,能得到“张三是学生”成立。
所谓“必要条件”,就是指条件的成立,是结论成立必须要的条件,没这个条件就不行。
所以就是条件不成立,则结论不成立。或者反过来,结论成立,则条件必然成立的关系。
例如“张三是学生”这个条件,是“张三是小学生”这个结论必须要的条件。
如果张三不是学生,那么张三当然不可能是小学生了。
所以“张三是学生”就是“张三是小学生”的必要条件,必须要的条件。
至于“充分不必要条件”就是指条件即是结论的充分条件,也不是结论的必要条件。
例如“张三是小学生”这个条件能充分的证明“张三是学生”这个结论,所以“张三是小学生”就是“张三是学生”的充分条件。
但是并不是必须要“张三是小学生”这个条件,才能得到“张三是学生”这个结论,张三是大学生、是中学生,也能证明张三是学生的结论,不必要是小学生。
所以“张三是小学生”就是“张三是学生”的充分不必要条件。
必要不充分条件,就是指条件既是结论的必要条件,也不是结论的充分条件。
例如“张三是学生”这个条件,是“张三是小学生”这个结论必须要的条件。
但是仅仅有“张三是学生”这个条件,还不能充分的证明“张三是小学生”这个结论,因为张三还可能是大学生、中学生。
所以“张三是学生”就是“张三是小学生”的必要不充分条件。
而充要条件,就是既是充分条件,又是必要条件。
什么是充分不必要条件?什么是必要不充分条件?什么是充分必要条件?
充分不必要:由A推出B,但是B不能推出A(也就是前面推出后面)
必要不充分:A不能推出B,但是B能推出A(后面推出前面)
充分必要:也就是充要条件,A推出B,也能推出A(前面后面都能推出)
必要条件和必要不充分条件有区别吗?
有区别。
必要条件是数学中的一种关系形式。如果没有A,则必然没有B;如果有A而未必有B,则A就是B的必要条件,记作B→A,读作“B含于A”。数学上简单来说就是如果由结果B能推导出条件A,我们就说A是B的必要条件。
含义不同:
充分条件:如果A能推出B,那么A就是B的充分条件。其中A为B的子集,即属于A的一定属于B,而属于B的不一定属于A,具体的说若存在元素属于B的不属于A,则A为B的真子集;若属于B的也属于A,则A与B相等。
必要条件:必要条件是数学中的一种关系形式。如果没有A,则必然没有B;如果有A而未必有B,则A就是B的必要条件,记作B→A,读作“B含于A”。数学上简单来说就是如果由结果B能推导出条件A,我们就说A是B的必要条件。
条件不同:
A是B的充分条件是“有A就有B”(即对B而言A是一个能“充分”推出B的前提)。
必要条件是“如果没有A那必定没有B”(即A这一条件的存在非常“必要”的)。
必要条件是数学中的一种关系形式。如果没有A,则必然没有B;如果有A而未必有B,则A就是B的必要条件,记作B→A,读作“B含于A”。数学上简单来说就是如果由结果B能推导出条件A,我们就说A是B的必要条件。
必要条件是数学中的一种关系形式。如果没有A,则必然没有B;如果有A而未必有B,则A就是B的必要条件,记作B→A,读作“B含于A”。数学上简单来说就是如果由结果B能推导出条件A,我们就说A是B的必要条件。
简单地说,不满足A,必然不满足B(即,满足A,未必满足B),则A是B的必要条件。例如:
1. A=“地面潮湿”;B=“下雨了”。
2. A=“认识26个字母”;B=“能看懂英文”。
3. A=“听过京剧”;B=“能体会到京剧的美”。
例子中A都是B的必要条件,确切地说,A是B的必要而不充分的条件:其一、A是B发生必需的;其二,A不必然导致B。在例子中,地面潮湿不一定就是下雨了;认识了26个字母不一定就能看懂英文;听过京剧未必能体会到京剧的美,这说明A不必然导致B。