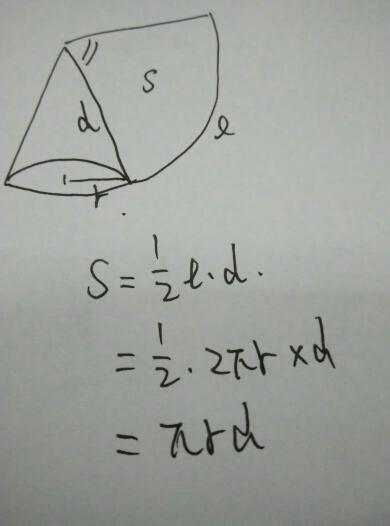正圆锥体的定义，到底是截面正三角形，还是顶点在低面的投影位于圆心？
正圆锥体就是底面截面是圆，且顶点与底面圆心的连线垂直于底面；也就是“
顶点在底面的投影位于圆心”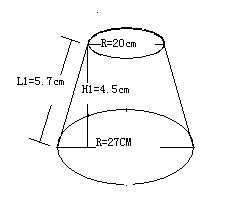
截面是三角形的不是圆锥体。
什么是正圆锥体
正圆锥体就是圆锥顶点的射影在底面圆的圆心。
通常所说的圆锥是指正圆锥，即圆锥顶点在底面的投影是圆心时的情况。一个直角三角形绕其中一条直角边旋转一周得到的几何体，这个直角三角形的斜边称为圆锥的母线。
正圆锥体的正视图和侧视图都是等腰三角形，俯视图是一个圆和圆心。
顶点在底面的投影不在圆心的圆锥称为斜圆锥。正圆锥可以由平面截圆锥面得到，斜圆锥则不能。而轴截面(即过圆锥轴的截面)是等边三角形或底面直径与母线相等的圆锥叫做等边圆锥。
扩展资料
生活中沙堆、漏斗、帽子、陀螺、斗笠、铅笔头、钻头、铅锤等都可以近似地看作圆锥。
（正）圆锥体展开图由一个扇形（圆锥的侧面）和一个圆（圆锥的底面）组成。母线长等于底面圆直径的圆锥，展开的扇形就是半圆。所有圆锥展开的扇形角度等于（底面直径÷母线）×180度。
圆锥的表面积由侧面积和底面积两部分组成。全面积（S）=S侧+S底。圆锥的体积等于与它等底等高的圆柱的体积的1/3。
参考资料来源：百度百科-圆锥
参考资料来源：百度百科-斜圆锥
参考资料来源：百度百科-等边圆锥
正圆锥的定义
正圆锥：顶点在底面的投影是底面圆心的圆锥体。
通俗点就是下面一个圆。上面的顶端到圆的任意一点距离相等。
