一、根号2加根号2等于多少?
√2+√2=2.828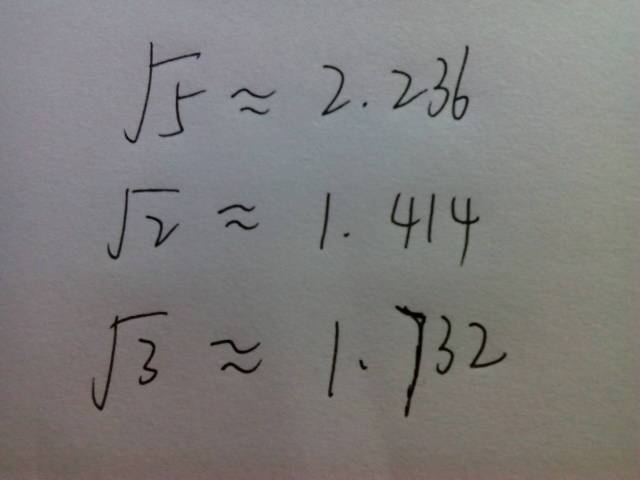
根号2的近似值为1.41421。
根号是用来表示对一个数或一个代数式进行开方运算的符号。若aⁿ=b,那么a是b开n次方的n次方根或a是b的1/n次方。被开方的数或代数式写在符号√ ̄的右边和符号上方一横部分的下方共同包围的区域中,而且不能出界。
在实数范围内,
(1)偶次根号下不能为负数,其运算结果也不为负。
(2)奇次根号下可以为负数。
扩展资料:
根号二的由来:
公元前500年,毕达哥拉斯学派的弟子希伯索斯(Hippasus)发现了一个惊人的事实,一个正方形的对角线与其一边的长度是不可公度的(若正方形的边长为1,则对角线的长不是一个有理数),这一不可公度性与毕氏学派的“万物皆为数”(指有理数)的哲理大相径庭。
这一发现使该学派领导人惶恐,认为这将动摇他们在学术界的统治地位,于是极力封锁该真理的流传,希伯索斯被迫流亡他乡,不幸的是,在一条海船上还是遇到毕氏门徒。被毕氏门徒残忍地投入了水中杀害。科学史就这样拉开了序幕,却是一场悲剧。
参考资料来源:百度百科-根号
二、根号2加根号2等于多少
根号2加根号2约等于2.828。
根号2的近似值为1.41421。
根号是用来表示对一个数或一个代数式进行开方运算的符号。若aⁿ=b,那么a是b开n次方的n次方根或a是b的1/n次方。被开方的数或代数式写在符号√ ̄的右边和符号上方一横部分的下方共同包围的区域中,而且不能出界。
在实数范围内,
(1)偶次根号下不能为负数,其运算结果也不为负。
(2)奇次根号下可以为负数。
扩展资料:
符号史
最早的根号“ ”源于字母“L”的变形(出自拉丁语latus的首字母,表示“边长”),没有线括号(即被开方数上的横线),后来数学家笛卡尔给其加上线括号,但与前面的方根符号是分开的,因此在复杂的式子显得很乱。
直至18世纪中叶,数学家卢贝将前面的方根符号与线括号一笔写成,并将根指数写在根号的左上角,以表示高次方根(当根指数为2时,省略不写。)。从而,形成了我们现在所熟悉的开方运算符号 。
由于在计算机中的输入问题,我们有时还可以使用sqrt(a,b)来表示a的b次方根。
参考资料来源:百度百科-根号
三、根号2加根号2等于多少?
根号2加根号2等于2√2。
√2+√2=2√2,其中√2已经是最简根式了,不可以化简,且2√2≈2.828。
根式介绍:
当根式满足以下三个条件时,称为最简根式。
①被开方数的指数与根指数互质。
②被开方数不含分母,即被开方数中因数是整数,因式是整式。
③被开方数中不含开得尽方的因数或因式。
在实数范围内:
(1)偶次根号下不能为负数,其运算结果也不为负。
(2)奇次根号下可以为负数。
不限于实数,即考虑虚数时,偶次根号下可以为负数,利用【i=√-1】即可。
写根号:先在格子中间画向右上角的短斜线,然后笔画不断画右下中斜线,同样笔画不断画右上长斜线再在格子接近上方的地方根据自己的需要画一条长度适中的横线,不够再补足。
四、根号二+根号二等于多少
根号2的近似值为1.41421.
根号是一个数学符号。根号是用来表示对一个数或一个代数式进行开方运算的符号。若aⁿ=b,那么a是b开n次方的n次方根或a是b的1/n次方。
扩展资料
1、写根号:
先在格子中间画向右上角的短斜线,然后笔画不断画右下中斜线,同样笔画不断画右上长斜线再在格子接近上方的地方根据自己的需要画一条长度适中的横线,不够再补足。(这里只重点介绍笔顺和写法,可以根据印刷体参考本条模仿写即可,不硬性要求)
2、写被开方的数或式子:
被开方的数或代数式写在符号左方v形部分的右边和符号上方一横部分的下方共同包围的区域中,而且不能出界,若被开方的数或代数式过长,则上方一横必须延长确保覆盖下方的被开方数或代数式。
3、写开方数或者式子:
开n次方的n写在符号√ ̄的左边,n=2(平方根)时n可以忽略不写,但若是立方根(三次方根)、四次方根等,是必须书写。
参考资料百度百科-根号