一、虚数i的平方是什么?
虚数i的平方等于负1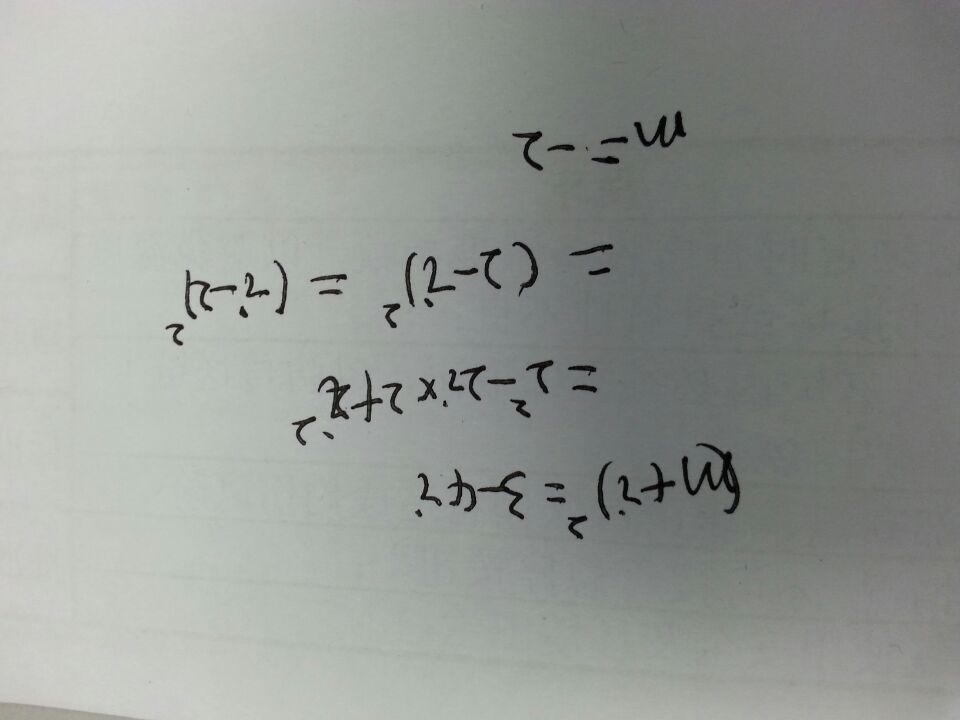
解析:
在数学中,虚数就是形如a+b*i的数,其中a,b是实数,且b≠0,i = - 1。虚数这个名词是17世纪著名数学家笛卡尔创立,因为当时的观念认为这是真实不存在的数字。后来发现虚数a+b*i的实部a可对应平面上的横轴,虚部b与对应平面上的纵轴,这样虚数a+b*i可与平面内的点(a,b)对应。
虚数符号:
1777年瑞士数学家欧拉(Euler,或译为欧勒)开始使用符号i表示虚数的单位。而后人将虚数和实数有机地结合起来,写成a+bi形式 (a、b为实数,a等于0时叫纯虚数,ab都不等于0时叫复数,b等于0时就是实数)。
而在工程运算中,为了不与其他符号(如电流的符号)相混淆,有时也用j或k等字母来表示虚数的单位。
通常,我们用符号C来表示复数集,用符号R来表示实数集。
二、虚数i的平方等于多少?
虚数的平方是虚数或负实数。
虚数 分为纯虚数和非纯虚数,纯虚数ai的平方=a的平方的负数,其中a是实数且不等于0。非纯虚数a+bi,a、b是实数且不等于0。
数这个名词是17世纪著名数学家笛卡尔创立,因为当时的观念认为这是真实不存在的数字。后来发现虚数a+b*i的实部a可对应平面上的横轴,虚部b与对应平面上的纵轴,这样虚数a+b*i可与平面内的点(a,b)对应。
扩展资料:
17世纪著名数学家笛卡尔所著《几何学》(法语:La Géométrie)一书中,命名其为nombre imaginaire(虚构的数),成为了虚数(imaginary number)一词的由来。
后来在欧拉和高斯的研究之后,后来发现虚数可对应平面上的纵轴,与对应平面上横轴的实数同样真实。虚数轴和实数轴构成的平面称复数平面,复数平面上每一点对应着一个复数。
在几何学上,复数平面的垂直轴表示虚数,它们与代表实数的水平轴垂直。查看虚数的方法之一是参考虑标准数线:往右侧正幅度增长,往左侧则负幅度减少。在x轴的0点处,往上升方向可绘制y轴的“正”虚数,然后向上增加;而“负”虚数则往下增加。
参考资料来源:百度百科——虚数
三、虚数的平方是()?
纯虚数ai的平方=-a^2,其中a是实数且不等于0
是负实数
非纯虚数a+bi,a,b是实数且不等于0
则(a+bi)^2=(a^2-b^2)+2abi
因为a和b都不等于0
所以a*b不等于0,所以这仍是一个虚数
所以选D
四、虚数的平方是什么?
虚数的平方是虚数或负实数。
虚数 分为纯虚数和非纯虚数,纯虚数ai的平方=a的平方的负数,其中a是实数且不等于0。非纯虚数a+bi,a、b是实数且不等于0。
可以将虚数bi添加到实数a以形成形式a + bi的复数,其中实数a和b分别被称为复数的实部和虚部。一些作者使用术语纯虚数来表示所谓的虚数,虚数表示具有非零虚部的任何复数。
虚数的数学价值:
在数学中,虚数就是形如a+b*i的数,其中a,b是实数,且b≠0,i = - 1。虚数这个名词是17世纪著名数学家笛卡尔创立,因为当时的观念认为这是真实不存在的数字。后来发现虚数a+b*i的实部a可对应平面上的横轴,虚部b与对应平面上的纵轴,这样虚数a+b*i可与平面内的点(a,b)对应。
虚数这个名词是17世纪著名数学家、哲学家笛卡尔创制,因为当时的观念认为这是真实不存在的数字。后来发现虚数可对应平面上的纵轴,与对应平面上横轴的实数同样真实。
虚数闯进数的领域时,人们对它的实际用处一无所知,在实际生活中似乎没有用复数来表达的量,因此在很长一段时间里,人们对它产生过种种怀疑和误解。笛卡尔称“虚数”的本意就是指它是虚假的;莱布尼兹则认为:“虚数是美妙而奇异的神灵隐蔽所,它几乎是既存在又不存在的两栖物。