一、正弦函数的周期公式
只有y=sinx才叫正弦函数，它的最小(短)周期t=2π
而正弦型函数y=asin(ωx+φ)+b或余弦型函数y=acos(ωx+φ)+b的求最小(短)周期的公式都是t=2π/|ω|,正余切型y=atan(ω+φ)+b,
y=acot(ω+φ)+b求最小(短)周期的公式都是t=π/|ω|.
二、周期怎么算数学公式？
f（x+a）=-f（x）周期为2a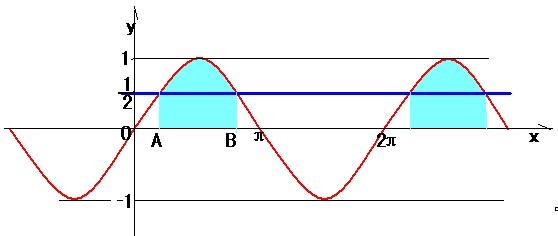
证明过程：因为f(x+a)=-f(x)，且f(x)=-f(x-a)，所以f(x+a)=f(x-a)，即f(x+2a)=f(x)，所以周期是2a。
sinx的函数周期公式T=2π，sinx是正弦函数，周期是2π
cosx的函数周期公式T=2π，cosx是余弦函数，周期2π。
tanx和cotx的函数周期公式T=π，tanx和cotx分别是正切和余切
secx 和cscx的函数周期公式T=2π，secx和cscx是正割和余割。
扩展资料：
y=Asin(wx+b) 周期公式T=2π/w
y=Acos(wx+b) 周期公式T=2π/w
y=Atan(wx+b) 周期公式T=π/w
重要推论：
如果函数f（x）（x∈D）在定义域内有两条对称轴x=a，x=b则函数f（x）是周期函数，且周期T=2|b-a|（不一定为最小正周期）。
如果函数f（x）（x∈D）在定义域内有两个对称中心A（a，0），B（b，0）则函数f（x）是周期函数，且周期T=2|b-a|（不一定为最小正周期）。
如果函数f（x）（x∈D）在定义域内有一条对称轴x=a和一个对称中心B（b， 0）（a≠b），则函数f（x）是周期函数，且周期T=4|b-a|（不一定为最小正周期）。
三、请问，正弦函数的周期怎么计算？
周期是参与正弦波动的粒子摆动一个完整波长的时间。
正弦曲线表达式为y=Asin(ωt+φ)，
其中A是波动幅度，φ是初始相位角，ω是波动的角速度（弧度/秒），周期T=2π/ω
ω=1时，周期为2π，波动的角速度ω越大，周期越短，频率越高。
四、正弦函数的周期怎么计算
若y=asin（ωx+φ）+b的周期t=2π/│ω│，
若y=│asin（ωx+φ）+b│时
当b=0时，t=π/│ω│；当b≠0时，t=2π/│ω│
希望能帮到你，如果有什么不懂还可以追问~~
五、正弦函数的周期怎么算？
周期=2π/|ω|
f(x)=Asin（ωx+ψ）
φ（初相位）：决定波形与X轴位置关系或横向移动距离（左加右减）
ω：决定周期（最小正周期T=2π/|ω|）
A：决定峰值（即纵向拉伸压缩的倍数）
正弦函数的性质：
（1）最值和零点
①最大值：当x=2kπ+（π/2） ，k∈Z时，y(max)=1
②最小值：当x=2kπ+（3π/2），k∈Z时，y(min)=-1
零值点：（kπ,0) ，k∈Z
（2）对称性
既是轴对称图形，又是中心对称图形。
1）对称轴：关于直线x=（π/2）+kπ，k∈Z对称
2）中心对称：关于点（kπ，0），k∈Z对称
六、函数周期的计算公式
（1）f（x+a）=-f（x）周期为2a。证明过程：因为f(x+a)=-f(x)，且f(x)=-f(x-a)，所以f(x+a)=f(x-a)，即f(x+2a)=f(x)，所以周期是2a。
（2）sinx的函数周期公式T=2π，sinx是正弦函数，周期是2π
（3）cosx的函数周期公式T=2π，cosx是余弦函数，周期2π。
（4）tanx和 cotx 的函数周期公式T=π，tanx和 cotx 分别是正切和余切
（5）secx 和cscx 的函数周期公式T=2π，secx 和cscx 是正割和余割。
扩展资料：
周期函数的判定方法分为以下几步：
（1）判断f（x）的定义域是否有界；
（2）根据定义讨论函数的周期性可知非零实数T在关系式f（x+T）= f（x）中是与x无关的，故讨论时可通过解关于T的方程f（x+T）- f（x）=0，若能解出与x无关的非零常数T便可断定函数f（x）是周期函数，若这样的T不存在则f（x）为非周期函数。
（3）一般用反证法证明。（若f（x）是周期函数，推出矛盾，从而得出f（x）是非周期函数）。
例：证f（x）=ax+b(a≠0）是非周期函数。
证：假设f（x）=ax+b是周期函数，则存在T（≠0），使之成立 ，a（x+T）+b=ax+b ax+aT-ax=0，aT=0 又a≠0，∴T=0与T≠0矛盾，∴f（x）是非周期函数。
例：证f（x）= ax+b是非周期函数。
证：假设f（x）是周期函数，则必存在T（≠0）对 ，有（x+T）= f（x），当x=0时，f（x）=0，但x+T≠0，∴f（x+T）=1，∴f（x+T） ≠f（x）与f（x+T）= f（x）矛盾，∴f（x）是非周期函数。
参考资料：百度百科——周期函数
