一、去心邻域什么意思?
去心邻域即在a的邻域中去掉a的数的集合,应用于高等数学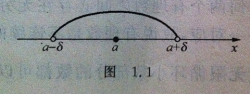
在拓扑学中,设A是拓扑空间(X,τ)的一个子集,点x∈A。如果存在集合U,满足 U 是开集,即 U∈τ;点x∈U;U 是A的子集,则称点 x 是 A 的一个内点,并称 A 是点 x 的一个邻域。
相关信息:
拓扑空间X,X的子集A是开集,当且仅当A是其中所有点的邻域。(显然由此可知,从邻域公理出发可以等价地定义拓扑空间)。
拓扑空间X,X的子集A和A°,A°是A的开核,当且仅当A° = {x | ∃U∈U(x),U⊆A}。
拓扑空间X,X的子集A和A’,A’是A的闭包,当且仅当A’ = {x | ∀U∈U(x),U∩A ≠ ∅}
二、请问在高等数学中,什么是去心邻域?最好能讲浅显点,不要复制定理~非常感谢!
首先,邻域是指某个数附近区域,如 3 的 δ 邻域是指满足 |x-3|<δ 的 x 集合,也就是 3-δ 去心邻域就是指不含中心点的邻域,如 3 的 δ 去心邻域是指满足 0<|x-3|<δ 的 x 集合, 也就是 { x | 3-δ 邻域,是指集合上的一种基础的拓扑结构。有邻域公理(邻域公理是现代数学拓扑结构的基础概念)、开邻域和闭邻域、去心邻域等的研究著作。邻域是一个特殊的区间,以点a为中心点任何开区间称为点a的邻域,记作U(a)。 去心邻域即在a的邻域中去掉a的数的集合,应用于高等数学。在拓扑学中,设A是拓扑空间(X,τ)的一个子集,点x∈A。如果存在集合U,满足 U 是开集,即 U∈τ;点x∈U;U 是A的子集,则称点 x 是 A 的一个内点,并称 A 是点 x 的一个邻域。 扩展资料: 邻域和去心邻域在拓扑学中:设A是拓扑空间(X,τ)的一个子集,点x∈A。如果存在集合U,满足U是开集,即U∈τ;点x∈U;U是A的子集,则称点x是A的一个内点,并称A是点x的一个邻域。若A是开(闭)集,则称为开(闭)邻域。 去心邻域即在a的邻域中去掉a的数的集合,应用于高等数学。在拓扑学中,设A是拓扑空间(X,τ)的一个子集,点x∈A。如果存在集合U,满足 U 是开集,即 U∈τ;点x∈U;U 是A的子集,则称点 x 是 A 的一个内点,并称 A 是点 x 的一个邻域。 只考虑点a邻近的点,不考虑点a,即考虑点集{x|a-δ ,即 。 扩展资料: 高等数学中,我们经常会用到一种特殊的开区间 ,称这个开区间为点a的邻域(neighbourhood),记为 ,即 ,并称点a为邻域的中心,δ为邻域的半径 。通常δ是较小的实数,所以,a的δ邻域表示的是a的邻近的点 。以a为中心的任何开区间都称为点a的邻域,记作U(a)。设δ是任一正数,则开区间(a-δ,a+δ)就是点a的一个邻域,这个邻域称为点a的δ邻域。 参考资料来源:百度百科-去心邻域三、邻域和去心邻域分别是什么?概念?怎么理解?
四、去心邻域什么意思?