一、圆柱体周长计算公式
所谓圆柱的周长,是指圆柱底面(截面)的周长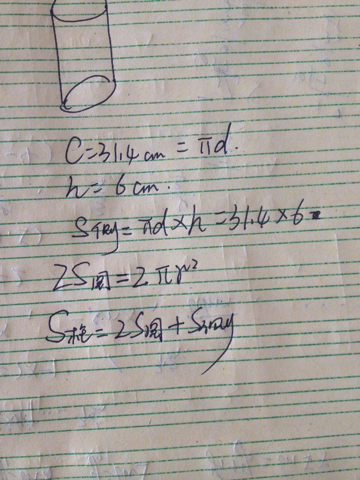
圆柱的底面周长是一个圆,那么
圆的周长=圆周率×直径
c=πd
圆的周长=圆周率×2×半径
c=2πr
在同一个平面内有一条定直线和一条动线,当这个平面绕着这条定直线旋转一周时,这条动线所成的面叫做旋转面,这条定直线叫做旋转面的轴,这条动线叫作旋转面的母线。如果母线是和轴平行的一条直线,那么所生成的旋转面叫做圆柱面。
扩展资料
组成名称
圆柱的两个完全相同的圆面叫做底面(又分上底和下底);圆柱有一个曲面,叫做侧面;两个底面的对应点之间的距离叫做高(高有无数条)。
特征:
1、圆柱的底面都是圆,并且大小一样。
2、圆柱两个面之间的垂直距离叫做高,把圆柱的侧面打开,得到一个矩形,这个矩形的一条边就是圆柱的底面周长。
与圆锥的关系
等底等高的圆锥积是圆柱体积的三分之一。
体积和高相等的圆锥与圆柱,圆锥的底面积是圆柱的三倍。
体积和底面积相等的圆锥与圆柱,圆锥的高是圆柱的三倍。
二、圆柱周长的计算公式
圆柱周长的计算公式:C=πd。如果母线是和相互平行,那么所生成的旋转面叫做圆柱面。如果用两个平行平面去截圆柱面,那么两个截面和圆柱面所围成的几何体称为圆柱。如果两个平行平面垂直于轴,那么称该圆柱为直圆柱(简称圆柱);如果两个平行平面不垂直于轴,那么称该圆柱为斜圆柱。
几何体(geometricsolid)亦称立体,是立体几何的基本概念之一。几何体概念产生于人们对客观世界中各种物体的数学抽象,当人们只考虑物体的形状、大小、位置关系等数学性质,而不考虑它的物理的、化学的、生物的、社会的等属性时,就获得几何体的概念,在几何学中,人们把若干几何面(平面或曲面)所围成的有限形体称为几何体,围成几何体的面称为几何体的界面或表面,不同界面的交线称为几何体的棱线,不同棱线的交点称为几何体的顶点,几何体也可看成空间中若干几何面分割出来的有限空间区域,立体几何首先研究的是一些较简单的几何体的几何性质,如多面体、旋转体以及它们的组合体等。
三、圆柱的周长怎么求?
所谓圆柱的周长,一般指的是圆柱的底面周长,圆柱底面的周长公式为:C=πd=2πr ,其中d为圆的直径,r为圆的半径,π是圆周率。
圆周长的计算
1、圆周长=圆周率×直径,字母公式:C=πd。
2、圆周长= 圆周率×半径×2,字母公式:C=2πr。
圆柱的分类
直圆柱
直圆柱也叫正圆柱、圆柱,其具有以下性质:
1、直圆柱的两个底面是半径相等的圆;
2、直圆柱的两个底面圆心的连线和两个底面相互垂直;
3、直圆柱的侧面展开图为矩形。
斜圆柱
斜圆柱具有以下性质:
1、斜圆柱的两个底面是半径相等的圆;
2、斜圆柱的两个底面圆心的连线和两个底面不垂直;
3、斜圆柱的侧面展开图为平行四边形。
四、圆柱的周长怎么算?
圆柱的周长公式就等于圆柱底面圆的周长公式,即:C=πd=2πr,公式中的C是周长,d是直径,r是半径,π是圆周率。
三角形的周长C = a+b+c(abc为三角形的三条边),四边形:C=a+b+c+d(abcd为四边形的边长),正方形:C=4a(a为正方形的边长),扇形的周长:C = 2R+nπR÷180˚(n=圆心角角度)=2R+kR (k=弧度)。
扩展资料
直圆柱也叫正圆柱、圆柱,其具有以下性质
(1)直圆柱的两个底面是半径相等的圆;
(2)直圆柱的两个底面圆心的连线和两个底面相互垂直;
(3)直圆柱的侧面展开图为矩形。
斜圆柱具有以下性质:
(1)斜圆柱的两个底面是半径相等的圆;
(2)斜圆柱的两个底面圆心的连线和两个底面不垂直;
(3)斜圆柱的侧面展开图为平行四边形。
五、圆柱的周长公式是什么?
圆柱的周长公式是:C=πd=2πr。
其中d为圆的直径,r为圆的半径,π是圆周率。
知道半径求周长:周长=2π×半径,c=2πr=6≈28r。
例:圆的半径是3米,周长C=2πr=2×3.14×3=18.84米。
知道直径求周:周长=3.14×直径,c=3.14×d=.314 d。
例:圆的直径是6米,周长C=πD=3.14×6=18.84米。
圆柱底面周长计算步骤
1、写出圆的周长公式
首先,要记得圆周长的计算公式C=2πr。
2、写出圆周率的值
其中π是圆周率,是有固定数值的,一般取值π=3.14。
3、通过直径计算半径r
其中r是一个圆的半径,因为一个圆的直径D=2r,直径等于2倍的半径,所以r=D/2,计算出圆的半径。
4、计算圆周长
由第二步我们得出圆的半径r,根据圆周长公式C=2πr=2*3.14*r,算出圆的周长。
六、圆柱的周长公式是多少?
圆柱的周长=底面直径xπ π的近似值为3.14。
公式说明:π是圆周率,约等于3.14,D是圆的直径,R是圆的半径。
举例:
1、圆的直径是6米,周长C=πD=3.14×6=18.84米。
2、圆的半径是3米,周长C=2πr=2×3.14×3=18.84米。
圆柱是由以矩形的一条边所在直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体。它有2个大小相同、相互平行的圆形底面和1个曲面侧面。其侧面展开是矩形。