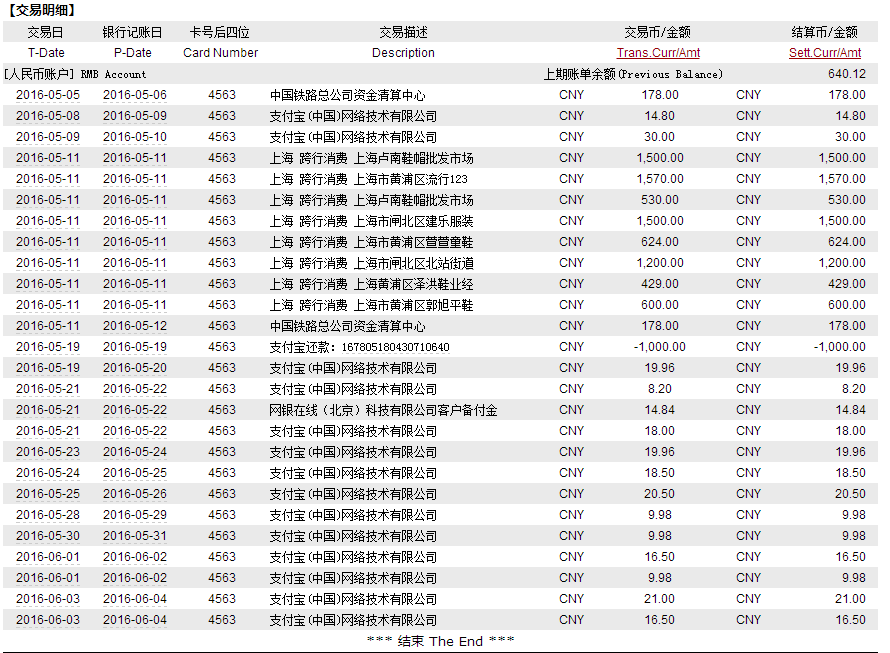
一、高等数学中,点在一个平面上的投影怎么算
简单计算一下即可,答案如图所示
二、点在平面上的投影点坐标怎么求
首先坐标定义为:确定天球上某一点的位置,在天球上建立的球面坐标系;点在平面上的投影点坐标求法:利用平面的法线,做出过点平行于平面法线的直线方程,然后和平面求交就可以了,比如设投影点N(x,y,z),向量MN=(x,y,z-1),平行于法向量(z-1)/1=0,z=1,向量M1N=(x,y,z),向量MN垂直于向量M1N,所以x^2+y^2+z(z-1)=0,z=1,x=y=0,所以投影点为:(0,0,1)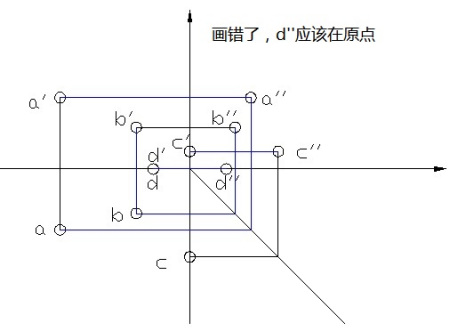
三、求点在平面上的投影
设投影点N(x,y,z)
向量MN=(x,y,z-1)
平行于法向量
(z-1)/1=0,z=1
向量M1N=(x,y,z)
向量MN垂直于向量M1N
x^2+y^2+z(z-1)=0
z=1,x=y=0
投影点:(0,0,1)
四、已知一点坐标和平面方程,求此点在平面上的投影点的坐标。
平面Ax+By+cZ+D=0的法向量为n=(A,B,C),M点在平面上的投影M‘的坐标(x2,y2,z2)。
所以Ax2+By2+cZ2+D=0(1),向量MM’=(x2-x1,y2-y1,z2-z1) 且MM’平行于 法向量n。即 (x2-x1)/A=(y2-y1)/B=(z2-z1)/C =k (2)。
平面法向量(a,b,c)。(x2-x1)/a=(y2-y1)/b=(z2-z1)/c。中点((x1+x2)/2,(y1+y2)/2,(z1+z2)/2)在平面上。a(x1+x2)/2+b(y1+y2)/2+c(z1+z2)/2+d=0。
扩展资料:
地理学上定义的坐标,即地理坐标系(Geographic Coordinate System),是使用三维球面来定义地球表面位置,以实现通过经纬度对地球表面点位引用的坐标系。一个地理坐标系包括角度测量单位、本初子午线和参考椭球体三部分。
一个点的位置,可以用一组数(有序数组)来描述。例如,在平面上,可以作两条相交的直线l1与l2;过平面上任一点M,作两条直线分别与l1、l2平行且与l2、l1交于P2、P1两点;这样,M点就可以用它沿平行于l1、l2的方向到l2、l1的有向距离P2M、P1M来表示。
这两个有向距离,称为点M的坐标,两条直线称为坐标轴,坐标轴的交点称为原点,当两直线相互垂直时,就是平面直角坐标系。
参考资料来源:百度百科-坐标
五、点在平面上的投影怎么求
设投影点N(x,y,z),向量MN=(x,y,z-1),平行于法向量(z-1)/1=0,z=1,向量M1N=(x,y,z),向量MN垂直于向量M1N,x^2+y^2+z(z-1)=0,z=1,x=y=0,则投影点:(0,0,1)。在空间中,平面是指到两点距离相同的点的轨迹。平面公式为A*(x-x0)+B*(y-y0)+C*(z-z0)=0,其定义为与固定点(x0,y0,z0)的连线垂直于固定方向(A,B,C)的所有的点的集合。这两种定义在数学上是一致的。
六、点到平面的投影怎么求
设平面的法向量是n,Q是这平面内任意一点,则空间点P到这个平面的距离:d=|QP·n|/|n|,这里QP表示以Q为起点、P为终点的向量。
距离d是向量QP在法向量n上投影的绝对值,即
d=|Pij
==|QP·n|/|n|