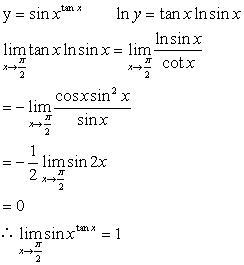一、arctanx的导数是什么arctanx怎么推导
1、arctanx的导数是:1/1+x2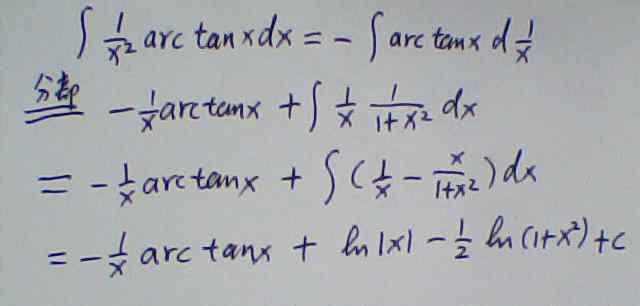
2、设y=arctanx,则x=tany。
因为arctanx′=1/tany′,且tany′=(siny/cosy)′=cosycosy-siny(-siny)/cos2y=1/cos2y。
则arctanx′=cos2y=cos2y/sin2y+cos2y=1/1+tan2y=1/1+x2。
所以arctanx的导数是1/1+x2。
二、arctan导数
arctanx的导数:y=arctanx,x=tany,dx/dy=secy=tany+1,dy/dx=1/(dx/dy)=1/(tany+1)=1/(1+x)。 扩展资料 Arctangent(即arctan)指反正切函数,反正切函数是反三角函数的一种,即正切函数的反函数。一般大学高等数学中有涉及。
三、arctanx的导数是什么?
解:令y=arctanx,则x=tany。
对x=tany这个方程“=”的两边同时对x求导,则
(x)'=(tany)'
1=sec²y*(y)',则
(y)'=1/sec²y
又tany=x,则sec²y=1+tan²y=1+x²
得,(y)'=1/(1+x²)
即arctanx的导数为1/(1+x²)。
反正切函数arctanx的求导过程
设x=tany
tany'=sex^y
arctanx'=1/(tany)'=1/sec^y
sec^y=1+tan^y=1+x^2
所以(arctanx)'=1/(1+x^2)