什么是子集,交集,并集,补集????
1、子集是一个数学概念:如果集合A的任意一个元素都是集合B的元素,那么集合A称为集合B的子集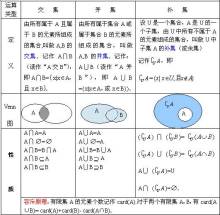
2、集合论中,设A,B是两个集合,由所有属于集合A且属于集合B的元素所组成的集合,叫做集合A与集合B的交集(intersection),记作A∩B。
3、给定两个集合A,B,把他们所有的元素合并在一起组成的集合,叫做集合A与集合B的并集,记作A∪B,读作A并B。
4、补集一般指绝对补集,即一般地,设S是一个集合,A是S的一个子集,由S中所有不属于A的元素组成的集合,叫做子集A在S中的绝对补集。在集合论和数学的其他分支中,存在补集的两种定义:相对补集和绝对补集。
扩展资料:
一、集合特性
1、确定性
给定一个集合,任给一个元素,该元素或者属于或者不属于该集合,二者必居其一,不允许有模棱两可的情况出现。
2、互异性
一个集合中,任何两个元素都认为是不相同的,即每个元素只能出现一次。有时需要对同一元素出现多次的情形进行刻画,可以使用多重集,其中的元素允许出现多次。
3、无序性
一个集合中,每个元素的地位都是相同的,元素之间是无序的。集合上可以定义序关系,定义了序关系后,元素之间就可以按照序关系排序。但就集合本身的特性而言,元素之间没有必然的序
二、运算定律
交换律:A∩B=B∩A;A∪B=B∪A
结合律:A∪(B∪C)=(A∪B)∪C;A∩(B∩C)=(A∩B)∩C
分配对偶律:A∩(B∪C)=(A∩B)∪(A∩C);A∪(B∩C)=(A∪B)∩(A∪C)
对偶律:(A∪B)^C=A^C∩B^C;(A∩B)^C=A^C∪B^C
同一律:A∪∅=A;A∩U=A
求补律:A∪A'=U;A∩A'=∅
对合律:A''=A
等幂律:A∪A=A;A∩A=A
零一律:A∪U=U;A∩∅=∅
吸收律:A∪(A∩B)=A;A∩(A∪B)=A
参考资料来源:百度百科-集合
并集的概念是什么?
并集就是把两个集合合并在一起组成的集合。
现有集合A和集合B,把他们所有的元素合并在一起组成的新集合,叫做集合A与集合B的并集,记作A∪B,读作A并B。集合A与集合B的并集中所有元素都可以在集合A或集合B中找到,不存在这两个集合没有的元素。
代数性质
并集运算满足交换律,即集合的顺序任意。
空集是并集运算的单位元。 即 ∅ ∪A=A。对任意集合A,可将空集当作零个集合的并集。
结合交集和补集运算,并集运算使任意幂集成为布尔代数。 例如,并集和交集相互满足分配律,而且这三种运算满足德·摩根律。 若将并集运算换成对称差运算,可以获得相应的布尔环。
什么是子集,交集,并集,补集
子集:对于集合A和集合B,如果集合A中的每个元素都属于集合B,那么集合A为集合B的子集,记作A⊆B(或B⊇A),用Venn图表示为
真子集:对于集合A和集合B,如果A⊆B,但存在元素属于集合B且不属于集合A,则称集合A为集合B的真子集,记作A⫋B。
交集:对于集合A和集合B,由属于集合A且属于集合B的所有元素组成的集合,称为A与B的交集,记作A∩B,用Venn图表示为
并集:对于集合A和集合B,由所有属于集合A或属于集合B的元素组成的集合,称为集合A与集合B的并集,记作A∪B,用Venn图表示为
补集:对于集合A,由全集U(一般地,如果一个集合含有所研究的问题中涉及的所有元素,那么就称这个集合为全集,通常记作U)中不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集,记作
用Venn图表示为
交集并集补集相关概念是什么?
交集:集合论中,设A,B是两个集合,由所有属于集合A且属于集合B的元素所组成的集合,叫做集合A与集合B的交集。
并集:给定两个集合A,B,把他们所有的元素合并在一起组成的集合,叫做集合A与集合B的并集。
补集:在集合论和数学的其他分支中,存在补集的两种定义:相对补集和绝对补集。
注意:学习补集的概念,首先要理解全集的相对性,补集符号∁UA有三层含义:
1、A是U的一个子集,即A⊊U。
2、∁UA表示一个集合,且∁UA⊊U。
3、∁UA是由U中所有不属于A的元素组成的集合,∁UA与A没有公共元素,U中的元素分布在这两个集合中。